The Steiner tree problem, named after Jakob Steiner, is a problem in combinatorial optimization.

The Steiner tree problem is superficially similar to the minimum spanning tree problem: given a set V of points (vertices), interconnect them by a network (graph) of shortest length, where the length is the sum of the lengths of all edges. The difference between the Steiner tree problem and the minimum spanning tree problem is that, in the Steiner tree problem, extra intermediate vertices and edges may be added to the graph in order to reduce the length of the spanning tree. These new vertices introduced to decrease the total length of connection are known as Steiner points or Steiner vertices. It has been proved that the resulting connection is a tree, known as the Steiner tree. There may be several Steiner trees for a given set of initial vertices.

The original problem was stated in the form that has become known as the Euclidean Steiner tree problem: Given N points in the plane, it is required to connect them by lines of minimum total length in such a way that any two points may be interconnected by line segments either directly or via other points and line segments.

For the Euclidean Steiner problem, points added to the graph (Steiner points) must have a degree of three, and the three edges incident to such a point must form three 120 degree angles. It follows that the maximum number of Steiner points that a Steiner tree can have is N-2, where N is the initial number of given points.

It may be further generalized to the metric Steiner tree problem. Given a weighted graph G(S,E,w) whose vertices correspond to points in a metric space, with edge weights being the distances in the space, it is required to find a tree of minimum total length whose vertices are a superset of set S of the vertices in G.

The most general version is Steiner tree in graphs: Given a weighted graph G(V,E,w) and a subset of its vertices 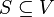, find a tree of minimal weight which includes all vertices in S. In an important special case of the graph problem, the Steiner tree problem for quasi-bipartite graphs, S is required to include at least one endpoint of every edge in G.

The Steiner tree problem has applications in circuit layout or network design. Most versions of the Steiner tree problem are NP-complete, i.e., thought to be computationally hard. In fact, one of these was among Karp's original 21 NP-complete problems. Some restricted cases can be solved in polynomial time. In practice, heuristics are used.

One common approximation to the Euclidean Steiner tree problem is to compute the Euclidean minimum spanning tree.

[edit] Outside the plane

The Steiner tree problem has also been investigated in multiple dimensions and on various surfaces. Algorithms to find the Steiner minimal tree have been found on the sphere, torus, projective plane, wide and narrow cones, and others.

Solution for three points; the Steiner point is in the middle—note there are no direct connections between A, B, C

Solution for four points—note that there are two Steiner points, S₁ and S₂

＝＝＝＝＝＝＝＝
From:http://ja.wikipedia.org/wiki/%E3%82%B7%E3%83%A5%E3%82%BF%E3%82%A4%E3%83%8A%E3%83%BC%E6%9C%A8

斯坦纳点 Steiner points

　　假设原来已经给定了n个点，库朗等指出需要引进的点数至多为n 2，此种点称为斯坦纳点。过每一斯坦纳点，至多有三条边通过。若为三条边，则它们两两交成120°角；若为两条边，则此斯坦纳点必为某一已给定的点，且此两条边交成的角必大于或等于120°。其中最小的网络称为已给定点的集合的最小斯坦纳树，记作SMT。若此SMT的斯坦纳点中有等于给定点的点，则称此SMT为退化的，此给定点称为退化点。

引自:http://baike.baidu.com/view/1464373.html