邻近算法

　　k-Nearest Neighbor algorithm
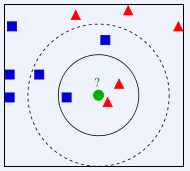
　　左图中，绿色圆要被决定赋予哪个类，是红色三角形还是蓝色四方形？如果K=3，由于红色三角形所占比例为2/3，绿色圆将被赋予红色三角形那个类，如果K=5，由于蓝色四方形比例为3/5，因此绿色圆被赋予蓝色四方形类。

　　K最近邻(k-Nearest Neighbor，KNN)分类算法，是一个理论上比较成熟的方法，也是最简单的机器学习算法之一。该方法的思路是：如果一个样本在特征空间中的k个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别，则该样本也属于这个类别。KNN算法中，所选择的邻居都是已经正确分类的对象。该方法在定类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。 KNN方法虽然从原理上也依赖于极限定理，但在类别决策时，只与极少量的相邻样本有关。由于KNN方法主要靠周围有限的邻近的样本，而不是靠判别类域的方法来确定所属类别的，因此对于类域的交叉或重叠较多的待分样本集来说，KNN方法较其他方法更为适合。

　　KNN算法不仅可以用于分类，还可以用于回归。通过找出一个样本的k个最近邻居，将这些邻居的属性的平均值赋给该样本，就可以得到该样本的属性。更有用的方法是将不同距离的邻居对该样本产生的影响给予不同的权值(weight)，如权值与距离成正比。

　　该算法在分类时有个主要的不足是，当样本不平衡时，如一个类的样本容量很大，而其他类样本容量很小时，有可能导致当输入一个新样本时，该样本的K个邻居中大容量类的样本占多数。因此可以采用权值的方法（和该样本距离小的邻居权值大）来改进。该方法的另一个不足之处是计算量较大，因为对每一个待分类的文本都要计算它到全体已知样本的距离，才能求得它的K个最近邻点。目前常用的解决方法是事先对已知样本点进行剪辑，事先去除对分类作用不大的样本。该算法比较适用于样本容量比较大的类域的自动分类，而那些样本容量较小的类域采用这种算法比较容易产生误分。

引自:百度百科 http://baike.baidu.com/view/1485833.html?fromTaglist
================
In pattern recognition, the k-nearest neighbors algorithm (k-NN) is a method for classifying objects based on closest training examples in the feature space. k-NN is a type of instance-based learning, or lazy learning where the function is only approximated locally and all computation is deferred until classification. The k-nearest neighbor algorithm is amongst the simplest of all machine learning algorithms: an object is classified by a majority vote of its neighbors, with the object being assigned to the class most common amongst its k nearest neighbors (k is a positive integer, typically small). If k = 1, then the object is simply assigned to the class of its nearest neighbor.

The same method can be used for regression, by simply assigning the property value for the object to be the average of the values of its k nearest neighbors. It can be useful to weight the contributions of the neighbors, so that the nearer neighbors contribute more to the average than the more distant ones. (A common weighting scheme is to give each neighbor a weight of 1/d, where d is the distance to the neighbor. This scheme is a generalization of linear interpolation.)

The neighbors are taken from a set of objects for which the correct classification (or, in the case of regression, the value of the property) is known. This can be thought of as the training set for the algorithm, though no explicit training step is required. The k-nearest neighbor algorithm is sensitive to the local structure of the data[citation needed].

Contents
[hide]
1 Algorithm
2 Parameter selection
3 Properties
4 See also
5 References
6 External links
 

[edit] Algorithm
 

Example of k-NN classification. The test sample (green circle) should be classified either to the first class of blue squares or to the second class of red triangles. If k = 3 it is classified to the second class because there are 2 triangles and only 1 square inside the inner circle. If k = 5 it is classified to first class (3 squares vs. 2 triangles inside the outer circle).
The training examples are vectors in a multidimensional feature space, each with a class label. The training phase of the algorithm consists only of storing the feature vectors and class labels of the training samples.

In the classification phase, k is a user-defined constant, and an unlabelled vector (a query or test point) is classified by assigning the label which is most frequent among the k training samples nearest to that query point.

Usually Euclidean distance is used as the distance metric; however this is only applicable to continuous variables. In cases such as text classification another metric such as the overlap metric (or Hamming distance) can be used.

A drawback to the basic "majority voting" classification is that the classes with the more frequent examples tend to dominate the prediction of the new vector, as they tend to come up in the k nearest neighbors when the neighbors are computed due to their large number[citation needed]. One way to overcome this problem is to weight the classification taking into account the distance from the test point to each of its k nearest neighbors.

[edit] Parameter selection
The best choice of k depends upon the data; generally, larger values of k reduce the effect of noise on the classification, but make boundaries between classes less distinct. A good k can be selected by various heuristic techniques, for example, cross-validation. The special case where the class is predicted to be the class of the closest training sample (i.e. when k = 1) is called the nearest neighbor algorithm.

The accuracy of the k-NN algorithm can be severely degraded by the presence of noisy or irrelevant features, or if the feature scales are not consistent with their importance. Much research effort has been put into selecting or scaling features to improve classification. A particularly popular approach is the use of evolutionary algorithms to optimize feature scaling[citation needed]. Another popular approach is to scale features by the mutual information of the training data with the training classes[citation needed].

In binary (two class) classification problems, it is helpful to choose k to be an odd number as this avoids tied votes.

[edit] Properties
The naive version of the algorithm is easy to implement by computing the distances from the test sample to all stored vectors, but it is computationally intensive, especially when the size of the training set grows. Many nearest neighbor search algorithms have been proposed over the years; these generally seek to reduce the number of distance evaluations actually performed. Using an appropriate nearest neighbor search algorithm makes k-NN computationally tractable even for large data sets.

The nearest neighbor algorithm has some strong consistency results. As the amount of data approaches infinity, the algorithm is guaranteed to yield an error rate no worse than twice the Bayes error rate (the minimum achievable error rate given the distribution of the data)[citation needed]. k-nearest neighbor is guaranteed to approach the Bayes error rate, for some value of k (where k increases as a function of the number of data points).

The k-NN algorithm can also be adapted for use in estimating continuous variables. One such implementation uses an inverse distance weighted average of the k-nearest multivariate neighbors. This algorithm functions as follows:

Compute Euclidean or Mahalanobis distance from target plot to those that were sampled.
Order samples taking for account calculated distances.
Choose heuristically optimal k nearest neighbor based on RMSE done by cross validation technique.
Calculate an inverse distance weighted average with the k-nearest multivariate neighbors.
From:http://en.wikipedia.org/wiki/K-nearest_neighbor_algorithm

=========

k最近邻居法采用向量空间模型来分类，概念为相同类别的案例，彼此的相似度高，而可以借由计算与已知类别案例之相似度，来评估未知类别案例可能的分类。

[编辑] 方法
目标：分类未知类别案例。
输入：待分类未知类别案例项目。已知类别案例集合D ，其中包含 j个已知类别的案例。
输出： 项目可能的类别。
其步骤为：

依公式计算 Item 与 D1、D2 … …、Dj 之相似度。得到Sim(Item, D1)、Sim(Item, D2)…。…。、Sim(Item, Dj)。
将Sim(Item, D1)、Sim(Item, D2)…。…。、Sim(Item, Dj)排序，若是超过相似度门槛t则放入邻居案例集合NN。
自邻居案例集合NN中取出前k名，依多数决，得到Item可能类别。

然而k最近邻居法因为计算量相当的大，所以相当的耗时，Ko与Seo[2]提出一算法TCFP(text categorization using feature projection)，尝试利用特征投影法（en:feature projection）来降低与分类无关的特征对于系统的影响，并借此提升系统效能，其实实验结果显示其分类效果与k最近邻居法相近，但其运算所需时间仅需k最近邻居法运算时间的五十分之一。

除了针对文件分类的效率，尚有研究针对如何促进k最近邻居法在文件分类方面的效果，如Han[1]等人于2002年尝试利用贪心法，针对文件分类实做可调整权重的k最近邻居法WAkNN (weighted adjusted k nearest neighbor)，以促进分类效果；而Li[3]等人于2004年提出由于不同分类的文件本身有数量上有差异，因此也应该依照训练集合中各种分类的文件数量，选取不同数目的最近邻居，来参与分类。

引自:http://zh.wikipedia.org/wiki/%E6%9C%80%E8%BF%91%E9%84%B0%E5%B1%85%E6%B3%95

=================

模糊knn算法

K最近邻(k-Nearest Neighbor，KNN)分类算法，是一个理论上比较成熟的方法，也是最简单的机器学习算法之一。该方法的思路是：如果一个样本在特征空间中的k个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别，则该样本也属于这个类别。KNN算法中，所选择的邻居都是已经正确分类的对象。该方法在定类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。 KNN方法虽然从原理上也依赖于极限定理，但在类别决策时，只与极少量的相邻样本有关。由于KNN方法主要靠周围有限的邻近的样本，而不是靠判别类域的方法来确定所属类别的，因此对于类域的交叉或重叠较多的待分样本集来说，KNN方法较其他方法更为适合。
　　KNN算法不仅可以用于分类，还可以用于回归。通过找出一个样本的k个最近邻居，将这些邻居的属性的平均值赋给该样本，就可以得到该样本的属性。更有用的方法是将不同距离的邻居对该样本产生的影响给予不同的权值(weight)，如权值与距离成正比。
　　该算法在分类时有个主要的不足是，当样本不平衡时，如一个类的样本容量很大，而其他类样本容量很小时，有可能导致当输入一个新样本时，该样本的K个邻居中大容量类的样本占多数。因此可以采用权值的方法（和该样本距离小的邻居权值大）来改进。该方法的另一个不足之处是计算量较大，因为对每一个待分类的文本都要计算它到全体已知样本的距离，才能求得它的K个最近邻点。目前常用的解决方法是事先对已知样本点进行剪辑，事先去除对分类作用不大的样本。该算法比较适用于样本容量比较大的类域的自动分类，而那些样本容量较小的类域采用这种算法比较容易产生误分。

http://wenda.tianya.cn/wenda/thread?tid=7dc3fa24f593fb59